Pairs of angles can be related, and these relationships can aid in finding the value of an unknown angle.
Complementary Angles
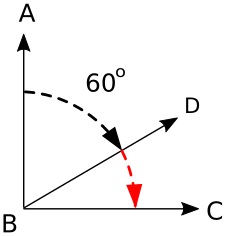
When the sum of two angles equals 90 degrees, the angles are complementary. Because the sum of the angles equals 90 degrees, you can subtract the known angle from 90 degrees to determine the value of the unknown angle.
In the example shown above, if angle ABD is 60 degrees, angle DBC must be 90 - 60, which is 30 degrees.
Supplementary Angles
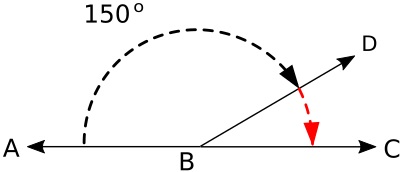
When the sum of two angles equals 180 degrees (a straight line), the angles are supplementary. Because the sum of the angles equals 180 degrees, you can subtract the known angle from 180 degrees to determine the value of the unknown angle.
In the example shown above, if angle ABD is 150 degrees, angle DBC must be 180 - 150, which is 30 degrees.
Adjacent Angles
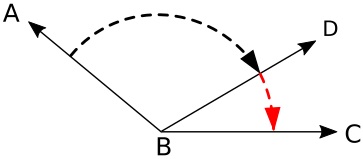
When two angles have a common vertex and a common side, they are adjacent angles. With adjacent angles, if you know the values of any two of the angles, you can determine the value of the unknown angle.
In the example shown above, two angles share vertex B and side D. If we know angle ABC is 150 degrees and angle ABD is 120 degrees, then angle DBC must be angle ABC - angle ABD, which is 30 degrees.
Vertical Angles
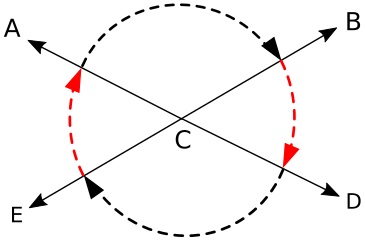
When two angles have a common vertex but don't share a common side, they are vertical angles. In this case "Vertical" does not mean up-down, it relates to the fact that they share the same Vertex.
Because the sides consist of two straight lines that pass through the same vertex, they create two pairs of equal angles. If one angle is 30 degrees, the opposite angle must also be 30 degrees. So the sum of the two opposite angles are 60 degrees.
Because a full circle is 360 degrees, 360 - 60 leaves 300 degrees. So the sum of the other two angles must be 300 degrees. And because the other two angles are also equal to each other, they must be 150 degrees each.
