Coils and direct current
Suppose that you have some wire that conducts electricity very well. What will happen if you wind a length of the wire into a coil and connect it to a source of dc, as shown in Fig. 13-2? The wire will draw a large amount of current, possibly blowing a fuse or over stressing a battery. It won't matter whether the wire is a single-turn loop, or whether it's lying haphazardly on the floor, or whether it's wrapped around a stick. The current will be large. In amperes, it will be equal to I = E/R, where I is the current, E is the dc voltage, and R is the resistance of the wire (a low resistance).
You can make an electromagnet, as you've already seen, by passing dc through a coil wound around an iron rod. But there will still be a large, constant current in the coil. The coil will probably get more or less hot, as energy is dissipated in the resistance of the wire. The battery, too, or power supply components, will become warm or hot.
If the voltage of the battery or power supply is increased, the wire in the coil, iron core or not, will get hotter. Ultimately, if the supply can deliver the necessary current, the wire will melt.
Coils and alternating current
Suppose you change the voltage source, connected across the coil, from dc to ac (Fig. 13-3). Imagine that you can vary the frequency of the ac, from a few hertz to hundreds of hertz, then kilohertz, then megahertz.
At first, the ac current will be high, just as it is with dc. But the coil has a certain amount of inductance, and it takes some time for current to establish itself in the coil. Depending on how many turns there are, and on whether the core is air or a ferromagnetic material, you'll reach a point, as the ac frequency increases, when the coil starts to get "sluggish." That is, the current won't have time to get established in the coil before the polarity of the voltage reverses.
At high ac frequencies, the current through the coil will have difficulty following the voltage placed across the coil. Just as the coil starts to "think" that it's making a good short circuit, the ac voltage wave will pass its peak, go back to zero, and then try to pull the electrons the other way.
This sluggishness in a coil for ac is, in effect, similar to dc resistance. As the frequency is raised higher and higher, the effect gets more and more pronounced. Eventually, if you keep on increasing the frequency of the ac source, the coil will not even begin to come near establishing a current with each cycle. It will act like a large resistance. Hardly any ac current will flow through it.
The opposition that the coil offers to ac is called inductive reactance. It, like resistance, is measured in ohms. It can vary just as resistance does, from near zero (a short piece of wire) to a few ohms (a small coil) to kiloohms or megaohms (bigger and bigger coils).
Like resistance, inductive reactance affects the current in an ac circuit. But, unlike simple resistance, reactance changes with frequency. And the effect is not just a decrease in the current, although in practice this will occur. It is a change in the way the current flows with respect to the voltage.
Reactance and frequency
Inductive reactance is one of two kinds of reactance; the other, called capacitive reactance, will be discussed in the next chapter. Reactance in general is symbolized by the capital letter X. Inductive reactance is indicated by the letter X with a subscript L: XL.
If the frequency of an ac source is given, in hertz, as f, and the inductance of a coil in henrys is L, then the inductive reactance is:
XL = 6.28fL
This same formula applies if the frequency, f, is in kilohertz and the inductance, L, is in millihenrys. And it also applies if f is in megahertz and L is in microhenrys. Just remember that if frequency is in thousands, inductance must be in thousandths, and if frequency is in millions, inductance must be in millionths.
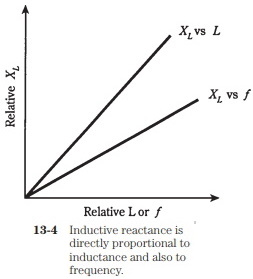
Inductive reactance increases linearly with increasing ac frequency. This means that the function of XL vs f is a straight line when graphed.
Inductive reactance also increases linearly with inductance. Therefore, the function of XL vs L also appears as a straight line on a graph.
The value of XL is directly proportional to f; XL is also directly proportional to L. These relationships are graphed, in relative form, in Fig. 13-4.
About the Author
Stan Gibilisco is one of McGraw-Hill's most prolific and popular authors, specializing in electronics and science topics. His clear, reader-friendly writing style makes his science books accessible to a wide audience, and his background in research makes him an ideal editor for professional references and course materials. He is the author of The Encyclopedia of Electronics; The McGraw-Hill Encyclopedia of Personal Computing; and several titles in the popular Demystified library of home-schooling and self-teaching books. His published works have won numerous awards. The Encyclopedia of Electronics was chosen a "Best Reference Book of the 1980s" by the American Library Association, which also named his McGraw-Hill Encyclopedia of Personal Computing a "Best Reference of 1996." Stan Gibilisco maintains a Web site at www.sciencewriter.net.
Quickly and easily learn the hows and whys behind basic electricity, electronics, and communications - at your own pace, in your own home Teach Yourself Electricity and Electronics, Fourth Edition offers easy-to-follow lessons in electricity and electronics fundamentals and applications from a master teacher, with minimal math, plenty of illustrations and practical examples, and test-yourself questions that make learning go more quickly. Great for preparing for amateur and commercial licensing exams, this trusted guide offers uniquely thorough coverage, ranging from dc and ac concepts and circuits to semiconductors and integrated circuits.
The best course - and source - in basic electronics
• Starts with the basics and takes you through advanced applications such as radiolocation and robotics
• Packed with learning-enhancing features: clear illustrations, practical examples, and hundreds of test questions
• Helps you solve current-voltage-resistance-impedance problems and make power calculations
• Teaches simple circuit concepts and techniques for optimizing system efficiency
• Explains the theory behind advanced audio systems and amplifiers for live music
• Referenced by thousands of students and professionals
• Written by an author whose name is synonymous with clarity and practical sense
New to This Edition: Updated to reflect the latest technological advances in:
• Wireless technology
• Computers and the Internet
• Transducers
• Sensors
• Robotics
• Audio systems
• Navigation
• Radiolocation
• Integrated circuits
ReaderRobert L. Young says; "I'm doing course development for a community college. I have evaluated a number of books in order to select one to use as the textbook. The course title is "Basic Electronics and Troubleshooting." This is the book I selected for the course. It has all of the material needed for the course requirements. It has good, understandable illustrations. It includes end of chapter quizzes with answers in the back. The book has far more material than we will be covering in the class, and includes more advanced math than the students will need for this particular course, but I don't see that as a disadvantage. I'll give them reading assignments relevant to the course work, and let them know that the book contains a lot of valuable, additional information for more advanced study. When I say "more advanced study," don't get me wrong; this book isn't a text for a graduate engineering course. It does, however, contain substantially more information than can be covered in a 72 hour Basic Electronics class. All the basics are well-covered and understandable, and the book allows you to keep moving forward from there."



