In an AC circuit with a capacitor or an inductor there is a phase shift between voltage and current. In this article you learn how to calculate the amount of that phase shift.
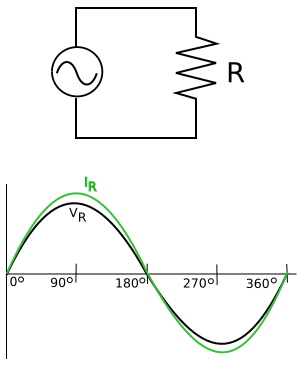
In a purely resistive AC circuit, current and voltage are in phase.
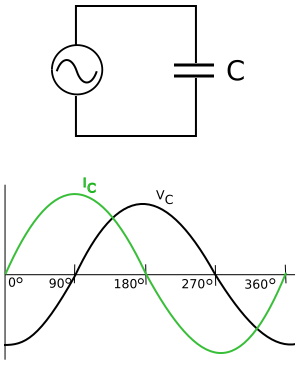
In a purely capacitive AC circuit, current leads voltage by 90 degrees. There is a +90 degree phase shift.
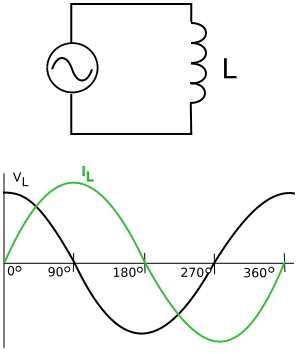
In a purely inductive AC circuit, current lags voltage by 90 degrees. There is a -90 degree phase shift.
Series Resistor Capacitor Circuit
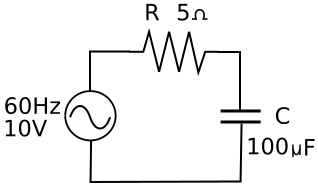
In an AC RC circuit (resistive/capacitive) circuit, current leads voltage by less than 90 degrees. In a circuit with 5 ohm resistor and a 100 uF capacitor, there will be a 79.3 degree phase shift.
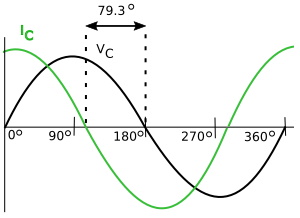
How to Calculate Phase Shift in a Series RC Circuit
To calculate the phase in a series RC circuit, use R (resistance) as one side, and Xc (capacitive reactance) as the other side of a right triangle, and use the trigonometry arctangent function (symbol tan-1) to calculate the phase angle.
Note: the -1 does not mean tangent raised to the power of -1).
Let's use the values from the example above.
5 ohm resistor
.0001 farad capacitor
60 Hz frequency
10 volts
You'll need Xc in the formula, and the formula for Xc is:
1/2nfc.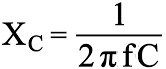
So, Xc = 1/ (2 * pi * 60 * 0.0001) = 26.525 ohms
Then to calculate the phase angle:
Phase_angle = tan-1 Xc/R = 79.3 degrees
<script> var r = 5; var c = .0001; var f = 60; var XC = 1/(2 * Math.PI * f * c); // Math.atan() function returns the // arctangent (in radians) var inrads = Math.atan(XC/5); // phase in degrees alert(inrads * (180/Math.PI)); </script>
Shown above is a short script to calculate phase shift in an RC circuit.
Series Resistor Inductor Circuit
In an AC RL circuit (resistive/ inductive) circuit, current lags voltage by less than 90 degrees. In a circuit with 5 ? of resistance and a 10 mH inductor, there will be a 37.0 degree phase shift.
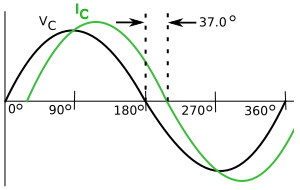
How to Calculate Phase Shift in a Series RL Circuit
Let's use the values from the example above.
5 ohm resistor
.01 henry inductor
60 Hz frequency
10 volts
You'll need XL in the forula, and the formula for XL is:
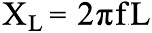
So, Xl = 2 * pi * 60 * 0.01 = 26.525 ohms
Then to calculate the phase angle:
Phase_angle = tan-1 Xl/R = 37.0 degrees
<script> // Xc is 2nfc var XC = 2 * Math.PI * 60 * .01; // Math.atan() function returns the // arctangent (in radians) var inrads = Math.atan(XC/5); // phase in degrees alert(inrads * (180/Math.PI)); </script>
Shown above is a short script to calculate phase shift in an RL circuit.

