Area of a Quadrilateral Calculator

A quadrilateral is any shape with four sides: squares, rectangles, parallelograms, and diamonds are examples. If you have a regular quadrilateral: square, rectangle, parallelogram or diamond, there are simple formulas to calculate the area. But if your quadrilateral has sides with all different lengths, different angles, and no parallel sides you can still calculate its area by viewing it as two triangles bucked up against one another. Find the area of each triangle, and then add them together.

All length units entered should be of the same measurement system, i.e. all metric or all English, and of the same base i.e. all centimeters or all meters, or all inches or all feet. Then the area output will those same units squared.

Since we're working with an irregular quadrilateral, I assume you can't easily measure a diagonal across the shape that would allow you to solve the two triangles using the length of their three sides. And it would also be difficult to determine the height of the two triangles to use the base times height formula.

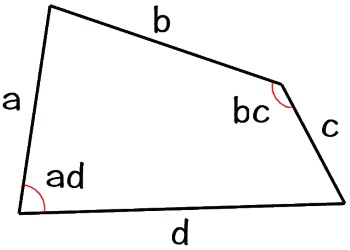
You can't find the area of an irregular quadrilateral using the length of the sides alone. To find the area of an irregular quadrilateral you need to know the length of all four sides, and the angles of two opposite angles.

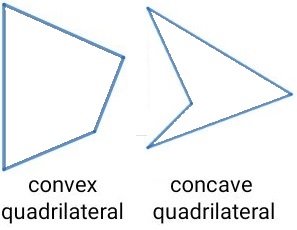
If you have a convex quadrilateral you would add the area of the two triangles together. If you have a concave quadrilateral you would subtract the area of the smaller triangle from the larger triangle to get the area of the quadrilateral.

With the sides and angles of the quadrilateral labeled as shown above, the formula for the area of a quadrilateral is:

Area = (Sin(ad) * (a * d)/2) + (Sin(bc) * (b * c)/2)

Note: Before using the results from this calculator, check this site's Web Site User Agreement. Also I would be greatful to hear your comments and suggestions about this app, or anything else. use the Contact Form.

RSS Feed

 Follow @Stephen Bucaro