A Spherical Cap is the part of a sphere that lies above or below a plane that passes through the sphere.
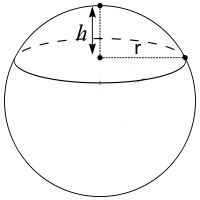
Formula for Volume of a Spherical Cap:
v = (1/6) pi h (3r2 + h2)
r = radius of the base of the cap
h = height of the cap
v = volume
a = area
Do not enter commas. Do not enter units. You can think of the unit as any length unit you like, English or Metric, but all values must be in the same units, and the result will be in those same units.
Note r is the radius of the base of the cap, not the radius of the sphere from which the cap is derived.
Almost all of the formulas for calculating the volume of a spherical cap use the radius of the sphere in the calculation. What if you don't know the radius of the sphere? You would need to construct two separated planes tangent to the surface of the sphere and run a perpendicular from each plane into the sphere. The center of the sphere would be where the two perpendiculars cross. From that you could calculate the radius of the sphere.
That is why this calculator uses a formula that uses the radius of the base of the cap, not the radius of the sphere.
Note: if the radius of the cap is the same size as the height, you have a hemisphere. Just calculate the volume of the sphere and divide by two. The height h of a cap cannot be more than the radius, because then you need to calculate the volume of the sphere and then subtract the volume of the cap on the other end of the sphere.
A note about significant digits. Multiplication and division use the following rule: The least number of significant digits in any number in the problem determines the number of significant digits in the result. So you have to round off the decimal places in the answer to the proper number of digits to the right of the decimal place. However rounding can result in a 0 as the last digit. The 0 then gets dropped creating a result with fewer significant digits.


