In practical electrical circuits, there is almost always some mutual inductance between or among coils when they are wound in a cylindrical shape. The magnetic fields extend significantly outside solenoidal coils, and mutual effects are almost inevitable. The same is true between and among lengths of wire, especially at very-high, ultra-high, and microwave radio frequencies. Sometimes, mutual inductance is all right, and doesn't have a detrimental effect on the behavior of a circuit. But it can be a bad thing.
Mutual inductance can be minimized by using shielded wires and toroidal inductors. The most common shielded wire is coaxial cable.
Coefficient of Coupling
The coefficient of coupling, specified by the letter k, is a number ranging from 0 (no coupling) to 1 (maximum possible coupling). Two coils that are separated by a sheet of solid iron would have essentially k = 0; two coils wound on the same form, one right over the other, would have practically k = 1.
Mutual Inductance
The mutual inductance is specified by the letter M and is expressed in the same units as inductance: henrys, millihenrys, microhenrys, or nanohenrys. The value of M is a function of the values of the inductors, and also of the coefficient of coupling.
For two inductors, having values of L1 and L2 (both expressed in the same size units), and with a coefficient of coupling k, the mutual inductance M is found by multiplying the inductance values, taking the square root of the result, and then multiplying by k. Mathematically,
M = k (L1L2)1/2
Effects of Mutual Inductance
Mutual inductance can operate either to increase the inductance of a pair of series connected inductors, or to decrease it. This is because the magnetic fields might reinforce each other, or they might act against each other.
When two inductors are connected in series, and there is reinforcing mutual inductance between them, the total inductance L is given in the formula:
L = L1 + L2 + 2M
where L1 and L2 are the values of the individual inductors, and M is the mutual indutance. All inductances must be expressed in the same size units.
Problem 10-5
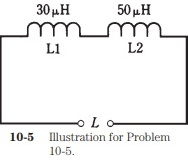
Suppose two coils, having values of 30 µH and 50 µH, are connected in series so that their fields reinforce, as shown in Fig. 10-5, and that the coefficient of coupling is 0.5. What is the total inductance of the combination?
First, calculate M from k. According to the formula for this, given above, M = .5(50 × 30)1/2 = 19.4 uH. Then the total inductance is equal to L = L1 + L2 + 2M + 30 + 50 + 38.8 = 118.8 uH, rounded to 120 uH because only two significant digits are justified.
When two inductors are connected in series and the mutual inductance is in opposition, the total inductance L is given by the formula
L = L1 + L2 - 2M
where, again, L1 and L2 are the values of the individual inductors.
Problem 10-6
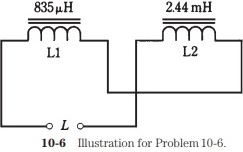
There are two coils with values L1 = 835 uH and L2 = 2.44 mH. They are connected in series so that their coefficient of coupling is 0.922, acting so that the coils oppose each other, as shown in Fig. 10-6. What is the net inductance of the pair?
First, calculate M. Notice that the coil inductances are specified in different units. Convert them both to microhenrys, so that L2 becomes 2440 uH. Then M = 0.922(835 x 2440)1/2 = 1316 uH. The total inductance is therefore L = L1 + L2 - 2M = 835 + 2440 - 2632 = 643 uH.
It is possible for mutual inductance to increase the total series inductance of a pair of coils by as much as a factor of 2, if the coupling is total and if the flux reinforces. Conversely, it is possible for the inductances of two coils to cancel each other. If two equal-valued inductors are connected in series so that their fluxes oppose, the result will be theoretically zero inductance.
About the Author
Stan Gibilisco is one of McGraw-Hill's most prolific and popular authors, specializing in electronics and science topics. His clear, reader-friendly writing style makes his science books accessible to a wide audience, and his background in research makes him an ideal editor for professional references and course materials. He is the author of The Encyclopedia of Electronics; The McGraw-Hill Encyclopedia of Personal Computing; and several titles in the popular Demystified library of home-schooling and self-teaching books. His published works have won numerous awards. The Encyclopedia of Electronics was chosen a "Best Reference Book of the 1980s" by the American Library Association, which also named his McGraw-Hill Encyclopedia of Personal Computing a "Best Reference of 1996." Stan Gibilisco maintains a Web site at www.sciencewriter.net.
Quickly and easily learn the hows and whys behind basic electricity, electronics, and communications - at your own pace, in your own home Teach Yourself Electricity and Electronics, Fourth Edition offers easy-to-follow lessons in electricity and electronics fundamentals and applications from a master teacher, with minimal math, plenty of illustrations and practical examples, and test-yourself questions that make learning go more quickly. Great for preparing for amateur and commercial licensing exams, this trusted guide offers uniquely thorough coverage, ranging from dc and ac concepts and circuits to semiconductors and integrated circuits.
The best course - and source - in basic electronics
• Starts with the basics and takes you through advanced applications such as radiolocation and robotics
• Packed with learning-enhancing features: clear illustrations, practical examples, and hundreds of test questions
• Helps you solve current-voltage-resistance-impedance problems and make power calculations
• Teaches simple circuit concepts and techniques for optimizing system efficiency
• Explains the theory behind advanced audio systems and amplifiers for live music
• Referenced by thousands of students and professionals
• Written by an author whose name is synonymous with clarity and practical sense
New to This Edition: Updated to reflect the latest technological advances in:
• Wireless technology
• Computers and the Internet
• Transducers
• Sensors
• Robotics
• Audio systems
• Navigation
• Radiolocation
• Integrated circuits
ReaderRobert L. Young says; "I'm doing course development for a community college. I have evaluated a number of books in order to select one to use as the textbook. The course title is "Basic Electronics and Troubleshooting." This is the book I selected for the course. It has all of the material needed for the course requirements. It has good, understandable illustrations. It includes end of chapter quizzes with answers in the back. The book has far more material than we will be covering in the class, and includes more advanced math than the students will need for this particular course, but I don't see that as a disadvantage. I'll give them reading assignments relevant to the course work, and let them know that the book contains a lot of valuable, additional information for more advanced study. When I say "more advanced study," don't get me wrong; this book isn't a text for a graduate engineering course. It does, however, contain substantially more information than can be covered in a 72 hour Basic Electronics class. All the basics are well-covered and understandable, and the book allows you to keep moving forward from there."
More Science, Technology, Engineering, and Mathematics Information:
• How to Find the Andromeda Galaxy
• Triac
• Reduce, Add, Subtract, Multiply and Divide Signed Fractions
• Basic Geometry Terminology: Point, Line, Line Segment, Ray, Plane, Plane Figure
• The Gravitational Force
• Magnetism
• Basic Laws and Analytical Methods for Circuit Analysis
• Electromagnetic Devices
• Circuit Analysis with Thevenin's theorem
• Inductors in Series and Parallel