All numbers can be classified as a certain type as illustrated by the venn diagram shown below. To understand we must start with the natural numbers shown inside the venn diagram.
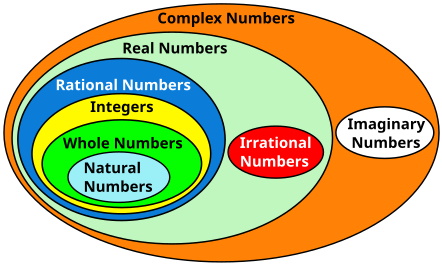
Types of Numbers Venn Diagram
Natural Numbers
The natural numbers are all positive numbers starting at 1 that have no decimal or fractional part. Sometimes they are called the counting numbers because people count by adding 1 to each natural number.
Some mathematicians think zero should be included in the set of natural numbers, but when counting a group of objects there is no zeroth object, and if you counted the first object as zero, the last number used would not be the number of objects in the group, and that is not natural.
Examples are: 1, 2, 3, 4, 5, ...
Whole Numbers
The whole numbers include all the natural numbers, along with zero. They are called whole numbers because they have no decimal or fractional part, or negative numbers.
Examples are: 0, 1, 2, 3, 4, ...
Integers
Integers include all the whole numbers. They have no decimal or fractional part, but they do include all negative numbers that have no decimal or fractional part.
Examples are: ... -4, -3, -2, -1, 0, 1, 2, 3, 4, ...
Rational Numbers
A rational number is any number that can be written as a fraction, where both the top number (numerator) and the bottom number (denominator) are integers. The denominator can not be equal to zero.
Rational numbers include integers because for example, the integer 4 can be written as 4/1.
A number with a decimal part is a rational number if the decimal part terminates because for example 3.28934 can be written with fractional part 28934/100000.
A number with a decimal part that does not terminate, but has a repeating pattern is a rational number because it can be written as a fraction. For example 0.3333333 ... can be written as 1/3. 3.142857142857142857 ... with the 142857 sequence that keeps repeating can be written as 1/7.
If the number cannot be written as a decimal with a repeating number or a repeating sequence of numbers, it is a not a rational number, it is an irrational number. For example π (pi) has a decimal part that is non-terminating and non-repeating, therefore it is an irrational number.
Rational numbers can are terminating decimals but irrational numbers are non-terminating.
1/3 = 0.3333333...
Numbers with a repeating pattern of decimals are rational because when you put them into fractional form, both the numerator and denominator become non-fractional whole numbers. This is because the repeating part of this decimal no longer appears as a decimal in rational number form.
Note: Sometimes we use π = 22/7, but this is not accurately pi, it is an approximation.
Irrational Numbers
An irrational number is defined as any number that cannot be expressed as a fraction or does not have terminating decimals or repeating decimals.
The ancient Greek mathematician Pythagoras taught that mathematics was the language of the gods and was therefore perfect. But his young student Hippasus discovered that the diagonal of a triangle whose sides are 1 unit long was the square root of 2, and that the square root of 2 could not be expressed as a rational number. When Hippasus revealed this, Pythagoras threw him overboard during a sea voyage and he drowned.
Real Numbers
A real number is any number that exists on the number line. All rational and irrational numbers exist on the number line. To precisely plot some real numbers on the number line you would have to zoom in infinitesimally close, never quite getting to the exact point, but according to the rules of algebra, they all have a place on the number line.
Imaginary Numbers
A rule of Algebra states that if we divide two negative numbers, we always get a positive result. But what if we take the square root of -1 (-1 divided by -1)? We get a negative number and does not have a tangible value. It cannot be plotted on the number line.
Despite the fact that we don't get a real number, we do get something useful. In fact, we use the symbol i to represent the square root of -1, and then define that i squared equals -1, and i to the fourth power equals 1.
Complex Numbers
A complex number is an element that is the sum of a real number plus an imaginary part. Every complex number can be expressed in the form a + bi, where a and b are real numbers. Complex numbers, are used in real world applications, such as advanced alternating current electronics and calculus.
More Science, Technology, Engineering, and Mathematics Information:
• Average Velocity and Instantaneous Velocity
• Properties of Algebra
• How to Prepare Microscope Slides
• Magnetism
• How to Observe Constellations
• Magnetism
• RMS Used in AC Circuit Analysis
• Direct Current
• Use a Resistor to Measure Inductance
• Basic Geometry Terminology: Point, Line, Line Segment, Ray, Plane, Plane Figure