Transformations stick around. Everything else we draw after drawing that mirrored character would also be mirrored. That might be inconvenient.
It is possible to save the current transformation, do some drawing and transforming, and then restore the old transformation. This is usually the proper thing to do for a function that needs to temporarily transform the coordinate system. First we save whatever transformation the code that called the function was using. Then the function does its thing, adding more transformations on top of the current transformation. Finally we revert to the transformation we started with.
The save and restore methods on the 2D canvas context do this transformation management. They conceptually keep a stack of transformation states. When you call save, the current state is pushed onto the stack, and when you call restore, the state on top of the stack is taken off and used as context's current transformation.
The branch function in the following example illustrates what you can do with a function that changes the transformation and then calls a function (in this case itself), which continues drawing with the given transformation.
<canvas width="600" height="300" style="border-style:solid;"></canvas>
<script>
let cx = document.querySelector("canvas").getContext("2d");
function branch(length, angle, scale)
{
cx.fillRect(0, 0, 1, length);
if(length < 8) return;
cx.save();
cx.translate(0, length);
cx.rotate(-angle);
branch(length * scale, angle, scale);
cx.rotate(2 * angle);
branch(length * scale, angle, scale);
cx.restore();
}
cx.translate(300, 0);
branch(60, 0.5, 0.8);
</script>
This function draws a treelike shape by drawing a line, then moving the center or the coordinate system to the end of the line, and then calling itself twice - first rotated to the left and then rotated to the right. Every call reduces the length of the branch drawn, and the recursion stops when the length drops below 8.
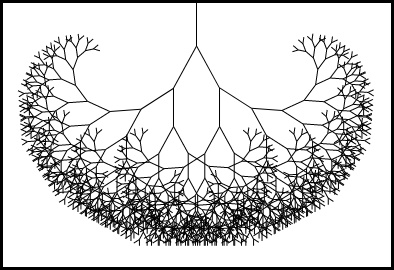
The result is a simple fractal.
If the calls to save and restore were not there, the second recursive call to branch would end up with the position and rotation created by the first call. It wouldn't be connected to the current branch but rather to the innermost, rightmost branch drawn by the first call. The resulting shape might also be interesting, but it is definitely not a tree.
This is an excerpt from:
JavaScript lies at the heart of almost every modern web application, from social apps like Twitter to browser-based game frameworks like Phaser and Babylon. Though simple for beginners to pick up and play with, JavaScript is a flexible, complex language that you can use to build full-scale applications.
This much anticipated and thoroughly revised third edition of Eloquent JavaScript dives deep into the JavaScript language to show you how to write beautiful, effective code. It has been updated to reflect the current state of JavaScript and web browsers and includes brand-new material on features like class notation, arrow functions, iterators, async functions, template strings, and block scope. A host of new exercises have also been added to test your skills and keep you on track.
As with previous editions, Haverbeke continues to teach through extensive examples and immerses you in code from the start, while exercises and full-chapter projects give you hands-on experience with writing your own programs. You start by learning the basic structure of the JavaScript language as well as control structures, functions, and data structures to help you write basic programs. Then you'll learn about error handling and bug fixing, modularity, and asynchronous programming before moving on to web browsers and how JavaScript is used to program them. As you build projects such as an artificial life simulation, a simple programming language, and a paint program, you'll learn how to:
• Understand the essential elements of programming, including syntax, control, and data
• Organize and clarify your code with object-oriented and functional programming techniques
• Script the browser and make basic web applications
• Use the DOM effectively to interact with browsers
• Harness Node.js to build servers and utilities
Isn't it time you became fluent in the language of the Web?
• All source code is available online in an inter-active sandbox, where you can edit the code, run it, and see its output instantly. Click here to learn more.
More Java Script Code:
• Easy Java Script Code for Sideways Slide show
• Display a Value in Currency Format
• Synchronous and Asynchronous Script Loading
• Let Your Web site Visitors Set Font Size
• Introduction to HTML5 Canvas
• Regular Expression Position Matching
• Easy Rollovers
• Easy HTML5 Drag and Drop
• Java Script Code to Re-arrange Items in a Select List
• Easy Slide Show Code With Linked Slides