Calculate The Points of an Equilateral Triangle
By Stephen Bucaro
An equilateral triangle is a triangle in which all three sides and all three angles
are congruent (all the same amount and all have the same relationship to each other).
All three internal angles are each 60 degrees.
Starting an equilateral triangle is easy, you just draw a line. A line has two points
P1(x1,y1) and P2(x2,y2). However, drawing the third point to create an exact equilateral
triangle requires a bit of calculation. One way to figure it out is to consider one
side as a vector. Then if you rotate the vector by 60 degrees, you will discover the
location of the third point.
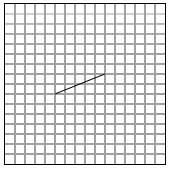
Lets assume the side we have is a line from P1(5,7) to P2(10,9). It would be easier
to rotate this vector if we translate it to the origin.
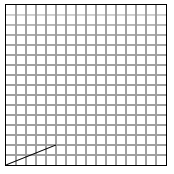
To do that we have to add a translation vector to it. The translation vector T(-5,-7)
brings P1 to the origin. When the translation vector T is applied to P2 we get P2'(5,2).
Now we can use the following matrix operation to rotate the vector 60 degrees:
x' = (x2 * cos(60)) - (y2 * sin(60))
y' = (x2 * sin(60)) + (y2 * cos(60))
x' = .768
y' = 5.33
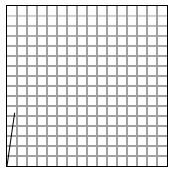
So, the three points of the equilateral triangle are p1(0,0) P2(5,2) and P3(.768,5.33).
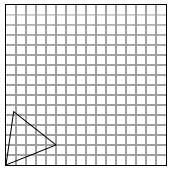
Next we can reverse the translate we used to move the original line to the origin.
The reverse translation vector would be T(5,7). When the translation vector T is applied
we get P1(5,7) P2(10,9) P3(5.768,12.33).
| 
About BTH
User Agreement
Privacy
Site Map
Contact
News Feeds
RSS Feed
Follow @Stephen Bucaro
General Web Design
