Boolean algebra is a system of mathematics in which the values of the variables can take on only one of two values, either 0 or 1 (sometimes referred to as false and true). The name "Boolean" comes from the name of its inventor, George Boole. Similar to regular algebra, Boolean algebra can be used to simplify a mathematical expression. And since computer logic is also a system in which the values of the inputs and outputs can take on only one of two values, Boolean algebra can be used to simplify logic circuits.
Boolean algebra consists of a set of postulates and a set of laws. I will list the postulates and laws in the tables below. In Boolean algebra the plus (+) symbol represents the logical OR operation, the dot (.) represents the logical AND operation, the prime (') represents the compliment operation (e.g. changing 0 to 1 or changing 1 to 0).
I know that to someone unfamiliar with Boolean algebra, the tables below look scary and boring, but you don't need to pay much attention to them at this point, I'm simply introducing them. You'll understand them more easily after I give examples of the use of some of these postulates and laws.
Boolean Algebra Postulates (sometimes called identities)
| A + 0 = A | Identity law | ORing a variable with 0 is always equal to the varable |
| A . 1 = A | Identity law | ANDing a variable with 1 is always equal to the varable |
| A + A = A | Identity law | ORing a variable with itself is always equal to that varable |
| A . A = A | Identity law | ANDing a varable with itself is always equal to that varable |
| A + 1 = 1 | Identity law | ORing a variable with 1 always results in 1 |
| A . 0 = 0 | Identity law | ANDing a varaible with 0 always results in 0 |
| A + A' = 1 | Complement law | ORing a variable with its complement always equals 1 |
| A . A' = 0 | Complement law | ANDing a variable with its complement always equals 0 |
| A'' = X | Complement law | A double complement of a variable is that variable |
Boolean Algebra Laws
| X+Y+Z = Z+Y+X | Commutative law of ORing | Changing the order of ORing variables does not change the result |
| X.Y.Z = Y.Z.X | Commutative law of ANDing | Changing the order of ORing variables does not change the result |
| X+(Y+Z) = (X+Y)+Z | Associative law of ORing | When ORing grouped variables changing the grouping does not change the result |
| X.(Y.X) = (X.Y).Z | Associative law of ANDing | When Anding grouped variables changing the grouping does not change the result |
| A(B+C) = AB+AC | Distributive law of ANDing over ORing | When ANDing a variable with a bracketed expression of ORed variables, you can remove the brackets and AND the variable with each individual ORed variable |
| A+(B.C) = (A+B).(A+C) | Distributive law of Oring over ANDing | When ORing a varaible with a bracketed expression of ANDed variables, you can remove the brackets and OR the variable with each individual ANDed variable |
| (X+Y)' = X'.Y' | de Morgan's law | The complement of Oring two variables is equivalent to complementing each variable and ANDing those two variables |
| (X.Y)' = X'+Y' | de Morgan's law | The complement of ANDing two variables is equivalent to complementing each variable and Oring those two variables |
| A+(A.B) = A | Redundance law | A combination of the result of using the Identity law and Distributive law |
| A.(A+B) = A | Redundance law | A combination of the result of using the Identity law and Distributive law |
Redundance law proof
A can be written as A.1 which the Identity law says equals 1 so A + AB can be written as A . (1+B). The Identity law says 1 + B = 1, so A . (1+B) can be written as A . 1 which the Identity law says equals A. In A . (A + B), the Distributive law says can be written as A.A + A.B and the Identity law says A . A = A, so we get A + AB, which as shown above equals A.
Converting Logic Diagram Into Boolean Expression
The primary use of Boolean algebra is to simplify or reduce the gate count of logic circuits, while still having them perform the same logic function. This is not difficult to do. Just work from left-to-right through the circuit block that you want to convert, expressing the logic of each gate in Boolean algebra. Lets convert the logic circuit shown below.
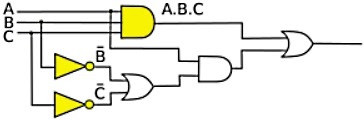
The inputs to the circuit are A,B,C. The out put of the fist AND gate is A.B.C. When expressing an AND operation in Boolean algebra, the "dot" symbol is optional). The output of the first inverter is B', the output of the second inverter is C'.
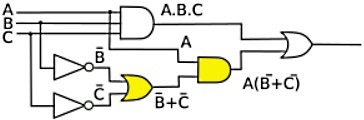
The outputs of the two inverters become inputs to an OR gate, the output of the OR gate then becomes B'+ C'. This is one input to an AND gate, ANDed with A, the output of the AND gate is A(B'+C').
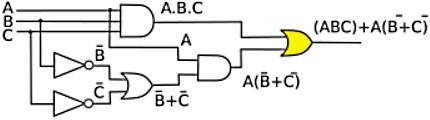
The output of the first AND gate, ABC along with the output of the second AND gate, A(B'+C'), becomes the input to an OR gate, resulting in the circuits output function being (ABC) + A(B'+C'). This is the Boolean statement that you would use the rules above to simplify.
Circuit Simplification Examples
Example 1:
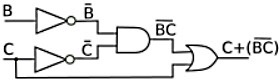
C+(BC)'
1. Use demorgan law to change AND to OR:
C+(B'+C')
2. Use assoiative law to put C with C':
(C+C')+B'
3. Use complement law to replace C+C' with 1
1+B'
4. Use identity law to eliminate the 1
B'
Example 2:
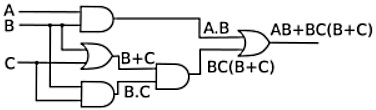
AB+BC(B+C)
1. Use distributive law of ANDing over ORingAB+BBC+BCC
2. Use identity law in second and third terms. ANDing a variable with itself is always equal to that variable.AB+BC+BC
3. USe identity law in second and third terms. ORing a variable with itself is always equal to that variable.AB+BC
4. Factor out B terms.B(A+C)
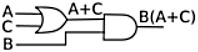
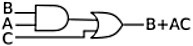
Example 3:
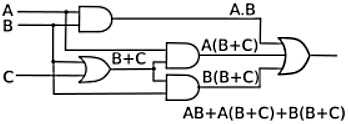
AB + A(B+C) + B(B+C)
1. Use distributive law of ORing over ANDing on second and third terms.
AB + AB + AC + BB + BC
2. Use A . A = A Identity law on first two and fourth terms.
AB + AC + B + BC
3. Use Redundance law on last two terms B + BC = B.
AB + AC + B
4. Use Redundance law on first and last terms AB + B = B.
B + AC
One of the most difficult parts of Boolean algebra, much like regular algebra, is to determine the order of operations. Which rules do apply in which order? The answer is, first try to eliminate any brackets from the statement. Secondly, try to eliminate any complementing (inverting) from the statement. Then try to simplify AND operations, then simplify OR operations. Basically, much like regular algebra, it takes practice.
More Computer Architecture Articles:
• How Computer Chips are Made
• Intel's Core 2 Processors
• Learn Assembly Language Programming on Raspberry Pi 400
• Operating System Processes
• The Android Operating System
• Round-Robin CPU Scheduling Algorithm
• Operating System Memory Paging Hardware Support
• Difference between Stack, Heap, and Queue
• Intel's Core i7 Processors
• Microcontroller Internal EEPROM (Electrically Erasable Programmable Read Only Memory) Memory